Graph Theory Fundamentals

In my previous post (can be found here), we discussed the importance of Graph Theory and how we find it everywhere in the world. In this post, we will explore the fundamental definitions along with examples to cement a foundational understanding of Graph Theory to aid in future posts going further in this study.

The structure and many of the definitions have been adapted from the lecture notes of Nathan Marianovsky’s Graph Theory course at UC Santa Cruz.

The Basics

Let’s first go over the primal definition of a graph.

I believe its best to understand this definition through an example. Consider the following graph .

Then we have our vertex set as seen in the image, and we represent each edge as a set of two vertices, so our edge set is . The reason we represent edges as a set is that the order of the vertices in an undirected edge does not matter; later with directed edges (edges with arrows), we account for the order.

Furthermore, we write an edge as for simplicity. Also when talking about different graphs, we tend to write the vertex and edge sets as and , respectively, in order to limit confusion.

Now let’s talk about adjacency and incidence of vertices and edges and also the concept of neighbors and neighborhoods.

These are some of the basic terminologies that we use in Graph Theory so it was important to introduce them first up. If we take the example from before, the vertices and are adjacent, is incident to the edge , and are edge adjacent, and the neighborhood of comprises of and .

A metric that is extremely important in the study of Graph Theory is the degree of a vertex defined below.

When the graph in discussion may be ambiguous, we denote the degree by , and this notion falls under basic Graph Theory notation. Furthermore, as an example, the degree of an entity or vertex of a social network shows the popularity of that entity since the more adjacent vertices or the bigger its neighborhood, the more that entity is connected with many other entities in the social network.

Now we shall define the subgraph which is essentially referring to graphs “contained” in the supergraph (or parent graph).

For example consider the graph again.

Now the following graph is a subgraph of , i.e. .

Notice that we are missing an edge from in . Meanwhile, the following graph is also a subgraph of , i.e. .

Notice that instead of missing just an edge, we are missing a vertex from in . Lastly, even is a subgraph of .

We call a subgraph a proper subgraph if we are missing at least a vertex or edge, or, in other words, the subgraph isn’t the original graph itself. So in the last example, both and are proper subgraphs of , but is not a proper subgraph of .

The subgraphs of a graph can tell us a lot about the graph itself, and this is explicitly seen in graph card decks, which we may discuss in the future. Also, the subgraph count can convey conclusions of the graph structure; for example, social networks tend to have a lot of triangle-shaped subgraphs.

This completes a basic introduction to the graph and some terminology. We haven’t discussed other types of graphs yet, but in later posts, we will go over the multigraph, pseudograph, and digraph which have different structures than the graph definition presented here which refers to the undirected graph.

Graph Traversal

The key to Graph Theory in the algorithmic sense is to understand graph traversal. By traversal, we mean to traverse edges to get from vertex to vertex. You might have heard of the Shortest Path Problem where we try to find the shortest connection between two vertices in a graph, or the Max-Flow Problem (some preliminary information can be found here) which indirectly uses traversals to determine a solution; these classes of problems all depend on traversing the graph in order to reach their conclusions. Although we won’t go into these algorithms, we will give a brief introduction to traversal.

Let’s dive into the definitions. We will be using basing all our examples from the following graph .

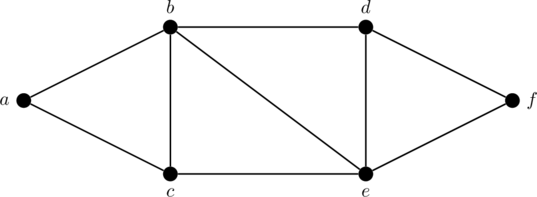
The first most basic method of traversal is called the walk as defined below.

This can be best seen through examples. Taking our graph from above, consider the walk going from to where we go up to , then , then , and then back to , and back to , and then back to , and then , and then . We can write this – walk as . Notice that we visited , , and twice and even went through the same edges twice. As the name suggests, a walk is really like a walk on the graph with absolutely no conditions.

Next with a few more restrictions on the structure of the traversal, we define the trail as follows.

In our last example of a walk, note that we repeated the edge , , and twice, so was not a trail. However, instead of going to after going back to from , if we rather go to and then , we get the trail , and we see that no edge is traversed more than once as required.

Then with further structure, we define the path, which I believe is the most important mode of traversal, again in the algorithmic sense.

Obviously was not a path since it wasn’t even a trail, and even is not a path since we visit vertex twice. However, is a valid path since we don’t traverse any edge or vertex more than once. Something interesting to note is that by not traversing vertices twice, we necessarily cannot have traversed any edge more than once, so a path can be defined as a walk with no vertex traversed twice.

Paths mean a lot in graph theory and algorithms as they are the most structured mode of traversal with least “overhead,” i.e. we never repeat any edge or vertex. Many times, we wish to optimize our mode of traversal, and so by repeating vertices and edges we are unnecessarily lengthening the traversal, so we look for paths from the start and destination.

Before continuing, let’s briefly define traversal length: which for some traversal (a walk, trail, or path) has length , i.e. we traverse edges.

Now let’s talk about closed traversals, i.e. we start and end at the same vertex. First we have the circuit.

For example, consider the circuit where we clearly don’t repeat any edge traversals and with length at least , and we start and end with the same vertex .

Again with further restrictions, we define the cycle which is the most common version of closed traversal similar to the paths.

For example, consider the cycle where we don’t repeat any vertices other than the first and last vertex (since its closed) and length is at least . Another way to define the cycle is to call it a circuit with no repeated vertices other than the first and last vertex in the sequence.

There are multiple algorithms that will be discussed in the future employing all these modes of graph traversal. Further, both the path and cycle fall under special graph families which will be discussed in the future. Nevertheless, knowing these basic traversal definitions is imperative in further study of Graph Theory.

Graph Connectedness

Now that we have talked about traversal, it makes sense why we would like to know if a traversal is even possible. We call this the reachability problem: to determine if we can we reach vertex from vertex in a graph. Before we go into the formal definition, let’s prove a key theorem first. It will additionally give you an initial taste of the Graph Theory proof dynamic which tends to be slightly more nuanced and semantic in its style.

To emphasize the principle utilized in the above proof, consider some walk which we depict below.

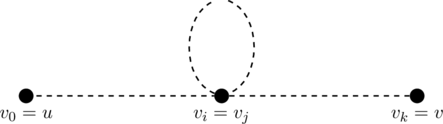
Due to the closed sub-walk from to (which are the same vertex), we can simply get rid of them to get the following walk.

We essentially are repeating this process till of course there are no repeated vertices, and at that point, we have derived a – path as required.

Now we define reachability as follows which should be obvious after our last theorem.

Since the most primitive and abstract mode of traversal is a walk, and by Theorem 1, we have shown that the existence of a walk implies a path, the above definition makes sense and is valid. Moreover, both Theorem 1 and Definition 13 stand testament to the importance of paths in Graph Theory.

Now, this leads into the important yet simple concept of connectedness which indicates whether a graph is connected or disconnected. We introduce this concept formally as follows.

A graph is connected if we can traverse to any other vertex from any vertex, and, on the other hand, a graph is disconnected if we cannot get from one vertex to another. As we will see now, the definition overcomplicates this notion which is quite clear in small examples, and it’s best to familiarize these key concepts through examples. Consider the following graph .

Now consider another graph depicted below.

We see that is connected because there is a path between every pair of vertices. However, is disconnected clearly just by seeing the two parts of the graph with no edges in between.

This concept of connectedness is deemed important in examples like network systems where if there is no line (path) connecting one system (vertex) to another, we have a problem if the network system is not connected.

The connectedness graph says quite a lot about the graph, but in the disconnected case we see that we can break down the graph into connected components as we saw the two components in the above disconnected graph. Essentially the connected components are the maximal connected subgraphs defined formally below.

Definition 15: A connected component is a connected subgraph of a graph such that it is not a subgraph of any other connected subgraph. Further, the number of connected components of is denoted by .

Also, many times we label connected components as just components when the context is clear. Further, the notion of not being a subgraph of any other connected subgraph provides for the maximal property of connected components. Although the definition makes it quite clear, consider the following disconnected graph .

The first component of is depicted below.

The second component of is depicted below.

And lastly the third component is shown below.

It’s clear to see why the above subgraphs are connected components of , and since we count three of them, we know in this example.

Moreover, the connected component count plays a crucial role in many applications like a power grid setting where we wish to know how many separate power grid systems in place in that state. If we consider every power line as an edge, and tower as a vertex, by determining the number of connected components in this graph we find the desired system count. This example emphasizes the importance of just the count of connected components along with the components themselves.

Before we continue, I wish to share another way to conceptualize the connected component. If we consider reachability as an equivalence relation, the equivalence classes of the graph are the connected components. This stems from the definition of connected graphs with regards to total reachability. It’s a cleaner way to think about connected components, but I refrain from keeping it as the formal definition due to the extra overhead of including relations.

Now that we have understood that graphs are in either a connected or disconnected state, many times theorems will apply to only connected graphs, so in the disconnected case we simply apply the theorem to the components. Also, if a graph as one component its anyway connected, so this thinking can be applied to all graphs and is a nice thing to keep in the back of your mind.

Just knowing a graph is connected implies a lot, but at the same time, there are so many possibilities. Thus we introduce the concept of connectivity which looks into how connected a graph is. The metric of vertex-connectivity is the least number of vertices required to remove from the graph to disconnect it, and similarly, we define edge-connectivity. In this way, we clearly have devised a way to express how connected a connected graph is, and this is important when we wish to determine the vulnerability of a system. For example in a chip, we wish for a high edge-connectivity so that if one wire malfunctions the entire system isn’t affected. The details of connectivity will be discussed in an upcoming post with formal definitions and comprehensive examples.

Looking Forward

Throughout this post, I have been mentioning topics that will follow this post to go deeper into the subject, so I’ll be posting accordingly. Something that wasn’t mentioned here was the crucial theory of trees which will be discussed in an upcoming post. Furthermore, I will be writing on some more advanced Graph Theory topics simultaneously, primarily focusing on my interests in the subject which tend to be more algorithm-based. The theory presented here is fairly sufficient to start going into graph algorithms on which I will tend to write about frequently as well. So keep on the lookout for upcoming posts in Graph Theory and Graph Algorithms!